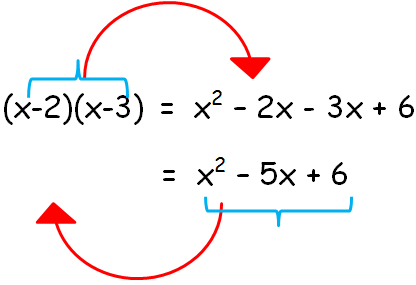
Root is nothing but the value of the variable that we find in the equation.To get a equation from its roots, first we have to convert the roots as factors. By multiplying those factors we will get the required polynomial.
2 and 3 are the roots of the polynomial then we have to write them as
To convert these as factors, we have to write them as
The product of those factors will give the polynomial. Because we have two factors, we will get a quadratic polynomial.
Number of factors = Highest exponent of the polynomial
Roots and zeroes are same.
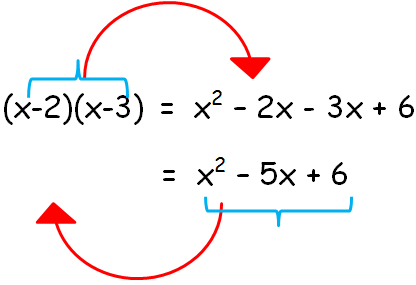
Write the polynomial function of the least degree with integral coefficients that has the given roots.
0, -4 and 5 are the values of x.
So we can write these values as
x = 0, x = -4 and x = 5
Now convert the values as factors.
(x - 0), (x + 4), (x - 5) are the factors of the required polynomial.
Number of factors = 3
Then, we will get a cubic polynomial.
By multiplying the above factors we will get the required cubic polynomial.
So, the required polynomial is
= (x - 0)(x + 4)(x - 5)
= (x-0)(x 2 - 5x + 4x - 20)
= x(x 2 - x - 20)
= x 3 - x 2 - 20x
Write the polynomial function of the least degree with integral coefficients that has the given roots.
3, 4/5 and 5/2 are the values of x. So we can write these values as
x = 3, x = 4/5 and x = 5/2
Now convert the values as factors.
(x - 3), (x - 4/5) and (x - 5/2) are the factors of the required polynomial.
Number of factors = 3
Then, we will get a cubic polynomial.
By multiplying the above factors we will get the required cubic polynomial.
So, the required polynomial is
= (x - 3)(x - 4/5)(x - 5/2)
= (x - 3)(x 2 - 5x/2 - 4x/5 + 2)
= (x - 3)(x 2 - 33x/10 + 2)
= (x - 3)(x 2 - 33x/10 + 2)
= x 3 - 33x 2 /10 + 2x - 3x 2 + 99x/10 - 6
Combine the like terms.
= x 3 - 63x 2 /10 + 119x/10 - 6
Write the polynomial function of the least degree with integral coefficients that has the given roots.
-5, 0 and 2i are the values of x.
Because 2i is the complex number, its conjugate must also be another root.
So, the required polynomial is having four roots.
Now convert the values as factors.
(x + 5), (x - 0), (x - 2i) and (x + 2i) are the factors of the required polynomial.
Number of factors = 4
Then, we will get a polynomial of degree 4 .
By multiplying the above factors we will get the required polynomial.
So, the required polynomial is
= (x + 5)(x - 0)(x - 2i)(x + 2i)
= x( x + 5)(x - 2i)(x + 2i)
= (x 2 + 5x)[x 2 - (2i) 2 ]
= (x 2 + 5x)(x 2 - 4i 2 )
= (x 2 + 5x)[(x 2 - 4(-1)]
= (x 2 + 5x)[(x 2 - 4(-1)]
= (x 2 + 5x)(x 2 + 4)
= x 4 + 4x 2 + 5x 3 + 20x
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
© All rights reserved. onlinemath4all.com